สถิติคืออะไรในบริบทคณิตศาสตร์ ? สรุปแบบย่อยง่าย
Table of Contents:
- สถิติและข้อมูลคืออะไร ?
- คำศัพท์สำคัญในสถิติ
- ประเภทของข้อมูล
- ตามแหล่งที่มาของข้อมูล
- ตามลักษณะของข้อมูล
- ประเภทของการวิเคราะห์ข้อมูล
- สถิติเชิงพรรณนา (Descriptive Statistics)
- สถิติเชิงอนุมาน (Inferential Statistics)
- การนำเสนอข้อมูล
- ข้อมูลเชิงคุณภาพ
- ข้อมูลเชิงปริมาณ
- ตัวอย่างข้อสอบ
สถิติและข้อมูลคืออะไร ?
เพื่อช่วยให้น้อง ๆ เข้าใจเรื่องสถิติคืออะไรในบริบทของวิชาคณิตศาสตร์ได้มากขึ้น ก่อนอื่นต้องเข้าใจนิยามความหมายของคำว่า ‘สถิติ’ กันก่อน !อธิบายแบบให้เข้าใจง่ายที่สุด สถิติศาสตร์ คือศาสตร์ที่ว่าด้วยการรวบรวม วิเคราะห์ และสรุปผลข้อมูล ซึ่งนำไปใช้ได้หลากหลาย เช่น การตัดสินใจ การแก้ปัญหาในชีวิตจริง หรือการพยากรณ์สถานการณ์ต่าง ๆ ยกตัวอย่าง เช่น
- การวิเคราะห์ผลการเรียนของนักเรียนทั้งห้องเพื่อดูว่าควรปรับปรุงตรงไหน
- การประเมินยอดขายสินค้าในธุรกิจ
- หรือแม้กระทั่งการคำนวณความน่าจะเป็นของทีมกีฬาที่จะชนะในแมตช์ใหญ่
ส่วนข้อมูลในสถิติคือทุกอย่างที่เราสนใจและสามารถบันทึกได้ เช่น ส่วนสูง, น้ำหนัก, คะแนนสอบ, หรือจำนวนครั้งที่เกิดเหตุการณ์บางอย่าง ดังนั้น สถิติจึงเป็นเครื่องมือสำคัญที่ช่วยให้เราสามารถเข้าใจความเป็นไปของสิ่งต่าง ๆ ได้ดียิ่งขึ้น
คำศัพท์สำคัญในสถิติ
ส่วนคำศัพท์ที่น้อง ๆ ควรจำให้ขึ้นใจ เพราะอาจต้องเจอในข้อสอบ A-Level เรื่องสถิติคณิตศาสตร์มีอะไรบ้างนั้น มักจะเป็นคำศัพท์พื้นฐานที่ใช้ในการรวบรวมข้อมูลต่าง ๆ เช่น- ประชากร (Population)
หมายถึงกลุ่มข้อมูลทั้งหมดที่เราสนใจศึกษา เช่น นักเรียนทุกคนในโรงเรียน, กลุ่มผู้ใช้งานแอปพลิเคชัน, กลุ่มพนักงานเอกชน ฯลฯ - ตัวอย่าง (Sample)
คือส่วนหนึ่งของประชากรที่เรานำมาวิเคราะห์ เช่น นักเรียน 100 คนจากโรงเรียนที่มีนักเรียนทั้งหมด 1,000 คน - ตัวแปร (Variable)
สิ่งที่เราสนใจศึกษา เช่น คะแนนสอบ, น้ำหนัก, ส่วนสูง - ข้อมูล (Data)
ค่าที่ได้จากการวัดตัวแปร เช่น คะแนนสอบ 85, 90, 95 - พารามิเตอร์ (Parameter)
ค่าที่แสดงลักษณะของประชากร เช่น ค่าเฉลี่ยน้ำหนักของคนในประเทศ - ค่าสถิติ (Statistic)
ค่าที่ได้จากตัวอย่าง เช่น ค่าเฉลี่ยน้ำหนักของคนในกลุ่มตัวอย่าง
ประเภทของข้อมูล
1. ตามแหล่งที่มาของข้อมูล
- ข้อมูลปฐมภูมิ (Primary Data) : ข้อมูลที่ได้จากการเก็บรวบรวมเอง เช่น การสำรวจ, การทดลอง
- ข้อมูลทุติยภูมิ (Secondary Data) : ข้อมูลที่ได้จากแหล่งอื่น เช่น รายงานสถิติที่เผยแพร่โดยหน่วยงาน
2. ตามลักษณะของข้อมูล
- ข้อมูลเชิงคุณภาพ (Qualitative Data) : ข้อมูลที่ไม่ใช่ตัวเลข เช่น สีตา, ประเภทอาหารที่ชอบ
- ข้อมูลเชิงปริมาณ (Quantitative Data) : ข้อมูลที่เป็นตัวเลข เช่น น้ำหนัก, ส่วนสูง
ประเภทของการวิเคราะห์ข้อมูล
ในเรื่องสถิติการวิเคราะห์ข้อมูลจะแบ่งออกเป็น 2 ประเภทหลัก คือ
1. สถิติเชิงพรรณนา (Descriptive Statistics)
การสรุปข้อมูลที่มีอยู่ให้เข้าใจง่าย เช่น การหาค่าเฉลี่ย การสร้างกราฟ การหาค่าสูงสุด-ต่ำสุด ตัวอย่างเช่น
- การหาคะแนนเฉลี่ยของนักเรียนทั้งชั้น
- การสร้างกราฟแท่งเพื่อแสดงการกระจายคะแนนสอบ
2. สถิติเชิงอนุมาน (Inferential Statistics)
การใช้ข้อมูลจากตัวอย่างเพื่อสรุปเกี่ยวกับประชากร เช่น
- การพยากรณ์แนวโน้มยอดขายสินค้าจากข้อมูลของร้านสาขาเดียว
- การคาดการณ์คะแนนเฉลี่ยของนักเรียนทั้งโรงเรียนจากการวิเคราะห์นักเรียนในบางห้อง
การนำเสนอข้อมูล
วิธีการนำเสนอข้อมูลในสถิติมีหลากหลายรูปแบบ เช่น
- ข้อมูลเชิงคุณภาพ : ใช้ตารางสรุปหรือกราฟแท่ง
- ข้อมูลเชิงปริมาณ : ใช้กราฟเส้น, ฮิสโตแกรม, หรือกล่องแสดงค่า
เทคนิค
- การอ่านกราฟฮิสโตแกรม ควรสังเกต "ความถี่" ของข้อมูลแต่ละช่วง
- การอ่านกราฟแท่ง ให้ดูว่าค่าบนแกน Y (แกนแนวตั้ง) แสดงถึงเรื่องอะไร เช่น จำนวนคน หรือเปอร์เซ็นต์
การวัดค่ากลางของข้อมูล
ส่วนนี้เจอบ่อยในข้อสอบและน้อง ๆ ต้องจำให้แม่น ! โดยการวัดค่ากลางมี 3 แบบหลัก ๆ ได้แก่- ค่าเฉลี่ยเลขคณิต (Arithmetic Mean)
คำนวณโดยการนำผลรวมของข้อมูลทั้งหมดมาหารด้วยจำนวนข้อมูล
ตัวอย่าง : คะแนนสอบ 70, 80, 90
ค่าเฉลี่ย = (70 + 80 + 90) ÷ 3 = 80 - ค่ามัธยฐาน (Median)
คือค่ากลางของข้อมูลเมื่อเรียงลำดับจากน้อยไปมาก
ตัวอย่าง : คะแนนสอบ 50, 60, 70, 80, 90
ค่ามัธยฐาน = 70 (อยู่ตรงกลางพอดี) - ฐานนิยม (Mode)
คือค่าที่เกิดซ้ำมากที่สุดในข้อมูล
ตัวอย่าง: คะแนนสอบ 50, 50, 60, 70, 80
ฐานนิยม = 50 (เพราะเจอบ่อยที่สุด)
ตัวอย่างข้อสอบ
ข้อ 1
มาแก้โจทย์ข้อนี้ไปทีละขั้นตอน
1. จากข้อมูล: a, b, 4, 4, 3, 3, 6, 5, 5, 8, 7, 7 โดยที่ a และ b เป็นจำนวนเต็มบวก
2. โจทย์บอกว่า ค่าพิสัย = มัธยฐาน = ค่าเฉลี่ยเลขคณิต ให้เราหาแต่ละค่า
3. หาค่าเฉลี่ยเลขคณิต
• ผลรวม = a + b + 4 + 4 + 3 + 3 + 6 + 5 + 5 + 8 + 7 + 7 (ตัวเลขบวกกัน = 52)
• ผลรวม = (a + b + 52)
• จำนวนข้อมูล = 12 ตัว
• ค่าเฉลี่ย = (a + b + 52)/12
4. หาค่ามัธยฐาน:
• เรียงข้อมูลจากน้อยไปมาก (สมมติว่า a < b): a, 3, 3, 4, 4, 5, b, 5, 6, 7, 7, 8
• b อยู่ตรงกลางระหว่าง 5 กับ 5 ดังนั้น b จึงเท่ากับ 5
• ค่าเฉลี่ย = a+5+52 / 12 = 5
• ดังนั้น a จึงเท่ากับ 3
• ข้อมูลมี 12 ตัว (เลขคู่) ดังนั้นมัธยฐานคือค่าเฉลี่ยของตำแหน่งที่ 6 และ 7
• มัธยฐาน = 5+5 / 2 = 5
5. หาค่าพิสัย:
• พิสัย = ค่ามากที่สุด - ค่าน้อยที่สุด
• ค่ามากที่สุดคือ 8 และค่าน้อยที่สุดคือ 3
• พิสัย = 8 - 3 = 5
6. จากโจทย์ พิสัย = มัธยฐาน = ค่าเฉลี่ย ดังนั้น: 8 - 3 = 5 = (3 + 5 + 52)/12
ดังนั้น a × b = 3 5 = 15
คำตอบคือ ข้อ ข. 15
ข้อ 2
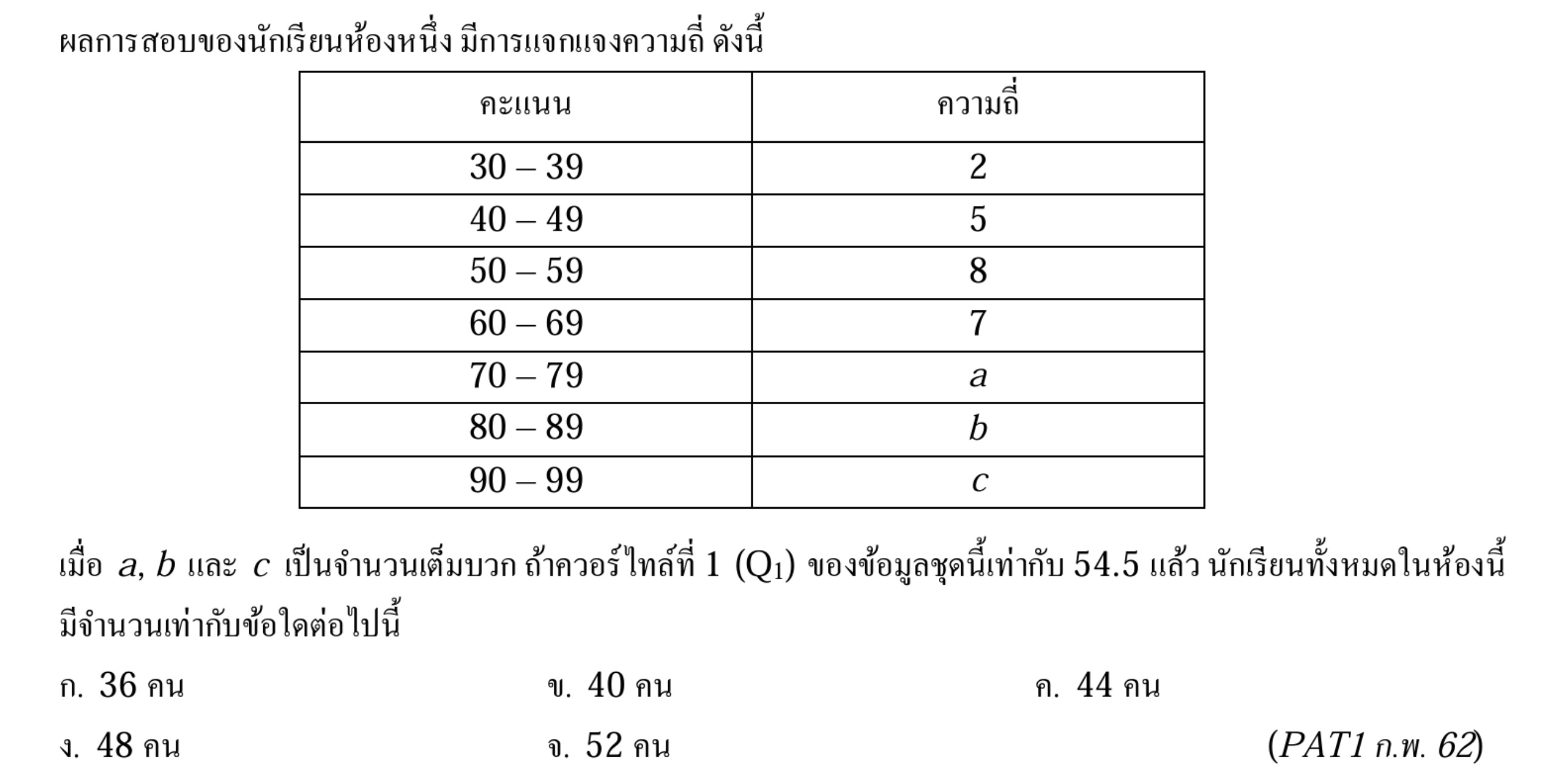
โจทย์ต้องการหาควอร์ไทล์ที่ 1 (Q1) = 54.5 และต้องหาจำนวนนักเรียนทั้งหมด
สร้างตารางแจกแจงความถี่สะสม
|
คะแนน |
ความถี่ |
ความถี่สะสม |
|
30-39 |
2 |
2 |
|
40-49 |
5 |
7 |
|
50-59 |
8 |
15 |
|
60-69 |
7 |
22 |
|
70-79 |
a |
22+a |
|
80-89 |
b |
22+a+b |
|
90-99 |
c |
22+a+b+c |
5. แทนค่าในสูตร:
ตำแหน่งควอร์ไทล์ที่ 1 = N / 4 = 22+a+b+c / 4
ความกว้างของอันตรภาคชั้น I = ขอบบน - ขอบล่าง
= 59.5-69.5 = 10
ค่าควอร์ไทล์ที่ 1 (Q1) = 54.5 ตกอยู่ชั้น 60-69
ขอบล่างชั้น Q1 = 59.5
ผลรวมความถี่ชั้นก่อน Q1 (Σƒ L, Q1 ) = 7
ความถี่ชั้น Q1 (ƒ Q1 ) = 8
ค่า Q1 = L + ( N/4 -Σƒ L, Q1 / ƒ Q1 ) I
54.5 = 49.5 + (((22+a+b+c / 4) - 7) / 8) (10)
4 = (22+a+b+c / 4 )- 7
a+b+c = 22
7. ดังนั้นจำนวนนักเรียนทั้งหมดจึงมี N = 22+a+b+c = 44 คน
คำตอบคือ ข้อ ค. 44 คน
ข้อ 3
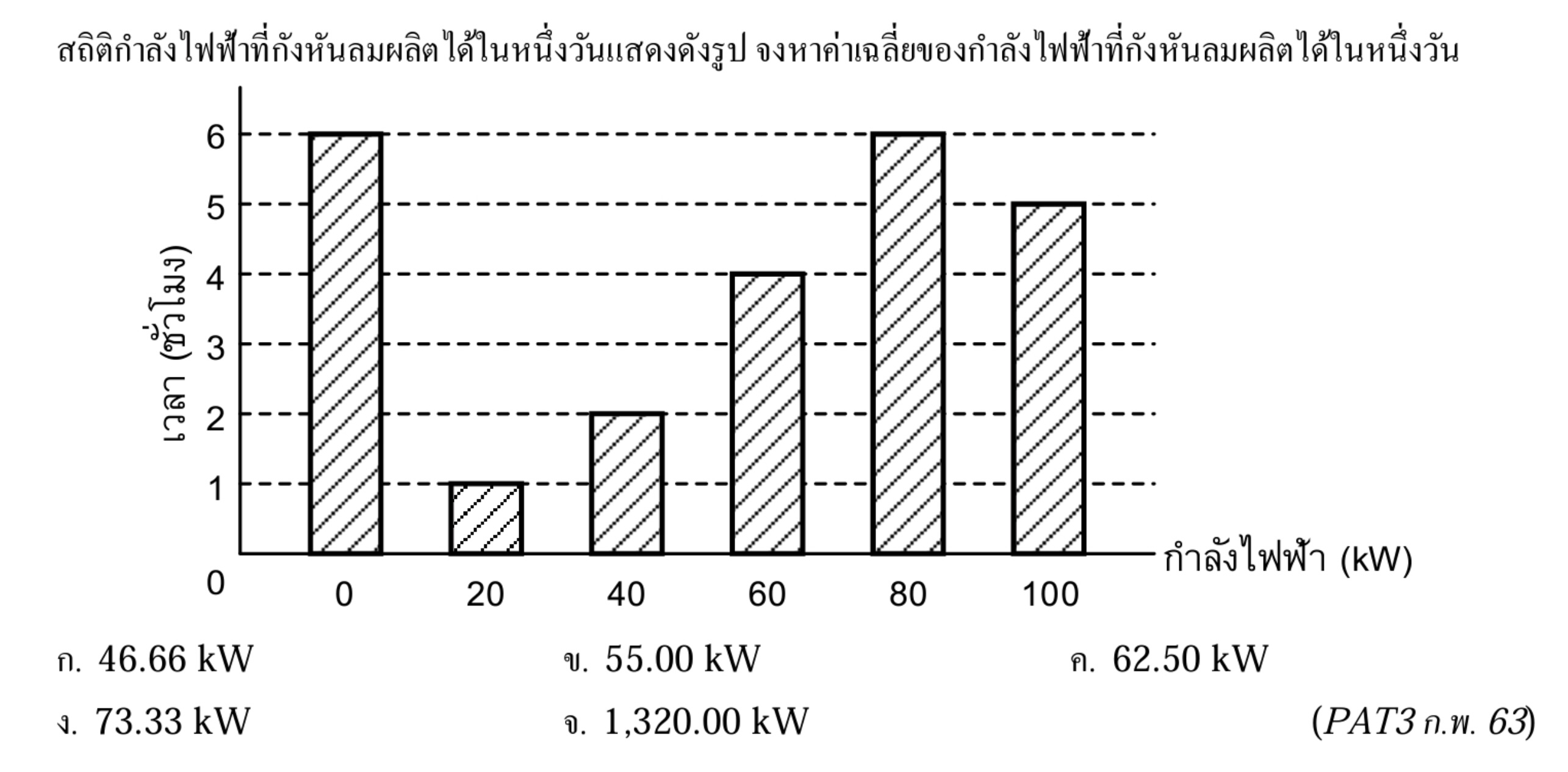
1. ข้อมูลจากกราฟ
- กำลังไฟฟ้า 0 kW มีความถี่ 6
- กำลังไฟฟ้า 20 kW มีความถี่ 1
- กำลังไฟฟ้า 40 kW มีความถี่ 2
- กำลังไฟฟ้า 60 kW มีความถี่ 4
- กำลังไฟฟ้า 80 kW มีความถี่ 6
- กำลังไฟฟ้า 100 kW มีความถี่ 5
2. การหาค่าเฉลี่ย (Mean) ใช้สูตร
ค่าเฉลี่ย = (ผลรวมของ [ค่า × ความถี่]) ÷ ผลรวมความถี่
3. คำนวณ
ผลรวมของ (ค่า × ความถี่)
(0 × 6) + (20 × 1) + (40 × 2) + (60 × 4) + (80 × 6) + (100 × 5)
= 0 + 20 + 80 + 240 + 480 + 500
= 1,320
ผลรวมความถี่
6 + 1 + 2 + 4 + 6 + 5 = 24
ค่าเฉลี่ย = 1,320 ÷ 24
= 55 kW
ดังนั้น ค่าเฉลี่ยของกำลังไฟฟ้าที่กังหันลมผลิตได้ในหนึ่งวัน = 55 kW
คำตอบคือ ข้อ ข. 55.00 kW
เตรียมสอบ A-Level อย่างมั่นใจกับคอร์สคณิตศาสตร์ของ Applied Physics
เมื่อน้อง ๆ เข้าใจภาพรวมแล้วว่าสถิติคืออะไรในบริบทของวิชาคณิตศาสตร์ รวมถึงสถิติคณิตศาสตร์ที่ใช้ในการสอบมีอะไรบ้าง ดังนั้น ถ้าน้อง ๆ อยากเข้าใจเรื่องสถิติในวิชาคณิตศาสตร์ให้มากขึ้น แนะนำเรียนเสริมคอร์สคณิตศาสตร์กับ Applied Physics เรามีคอร์สออนไลน์ให้เลือกเรียนมากมาย ครบทั้ง ม.ต้น ม.ปลาย ไม่ว่าจะเรียนเพิ่มเกรด หรือเรียนเพื่อเตรียมสอบ เนื้อหาแน่น ๆ พร้อมได้ตะลุยโจทย์ฝึกทำข้อสอบเพื่อสร้างความคุ้นเคย สอนโดยติวเตอร์ที่เชี่ยวชาญ มีประสบการณ์ และเทคนิคการสอนเหนือชั้น เพื่อให้น้องทำคะแนนสอบเพิ่มขึ้นได้จริง ต้องการสอบถามเพิ่มเติมเกี่ยวกับคอร์สเรียน โทรเลยที่ 02-3060867, 02-3060868, 02-3060869 และ 085-4925599 หรือแอดไลน์ @appliedphysics (มี @ ด้วย)
